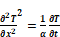
The heat transfer through the
layered constructions is assumed to be one dimensional. The heat conduction
equation 
is solved by using finite differences (Δt and Δx) to approximate the differential increments in time and distance; α is the thermal diffusivity. The smaller the finite increments, the more accurate the solution. The homogeneous layers are divided into lumps Δx thick, and the lumps are represented by the two-conductance/one-capacitance "T" circuits shown for each layer in Figure 2. Frequently the actual layer thicknesses as sufficiently thin that Δx can be taken as the layer thickness. However, at times the actual layer of homogeneous material must be divided into smaller thicknesses. See Section 2.4–Discretization Errors for the criterion used to determine Δx and Δt.
The temperatures of the mass nodes are updated every time step using the Euler explicit numerical integration method (see Press et al), whereby the change in temperature of the mass during the time step is based only on the boundary conditions at the beginning of the time step. The boundary conditions are the temperatures of the surrounding nodes and other heat flow sources.
To update Ti,1 in Figure 3, for example, if the rate of heat transfer into Ti,1 is equated to its rate of change in internal energy, resulting in the differential equation for mass temperature Ti,1
Equation 3

where Ti,1 is the surface layer mass temperature, and Tssi,1 is the temperature Ti,1 would have if steady state were reached:
Equation 4

Qsi' is given by Equation 1, ccci,1 by Equation 2, Ti,2 is the temperature of mass node 2, and τ is the time constant of mass node 1 given by:
Equation 5
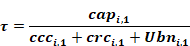
The heat capacity of layer-1 is capi,1 (Btu/ft2-F). Ubni,1 is the conductance between nodes 1 and 2, given by:
Equation 6
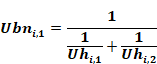
To integrate of Equation 3 over a time step, the Euler procedure assumes that the right hand side of the equation remains constant over the time step at its value at the beginning of the time step. In this case the mass temperature at the end of the time step becomes:
Equation 7
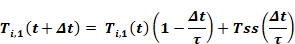
If the capacitance of any layer is zero (a convecting air layer for example) its updated temperature is set equal to Tss. That is, the temperature at the central node is determined by a steady state energy balance.
All of the mass nodes are updated in an analogous fashion each time step. The order in which the masses are updated is irrelevant because they are updated based only on the values of variables at the beginning of the time step, not on the values that may have been updated since.