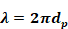
The temperatures predicted by Equation 7, which updates the layered mass temperatures, is subject to errors due to the finite lump size chosen to represent real wall homogeneous layers. It is also subject to errors due to the finite time step Δt. Similarly Equation 14 for updating the air mass temperature is subject to error due to the finite time step chosen.
Discretization errors can be made negligible by reducing the layer thicknesses and time step to very small values. However for practical run time minimization purposes it is useful to have large Δt and Δx layers, insofar as accuracy allows. The range of choices of Δt and Δx is narrowed if accurate results are only required for a limited range of frequencies of the driving boundary conditions. Only extremely thin lumped layers have the correct frequency response at high frequencies. To model environmental influences, 3 cycles/day (8-hr period sinusoid) is likely the highest frequency necessary to consider when determining the frequency response of buildings (Goldstein, Anderson and Subbarao). Higher frequencies may be desirable for accurately modeling things like control step changes. During the program development, accuracy was measured by analyzing the frequency response at 3 cycles/day.
The exact frequency response of a layered wall can be obtained using the matrix method (Section 3.7 of Carslaw & Jaeger) which gives the inside driving point admittance (from the inside air node), the outside driving point admittance, and the transfer admittance, for any frequency. The magnitude of the inside driving point admittance is the principle parameter used to assess algorithm accuracy.
At the frequency chosen, 3 cycles/day say, the exact driving point admittance of the real wall (with homogeneous layers) can be obtained from the matrix method. Similarly the exact driving point admittance of the lumped wall which the user has chosen to represent the real wall, can also be determined by the matrix method. Comparing these two results shows the accuracy of the lumping assumptions, independent of time step considerations.
The time discretization error associated with Equation 7 at the frequency chosen can be assessed by comparing the driving point admittance predicted by the CSE code, when the air node is driven with a sinusoidal temperature at the chosen frequency, to the theoretical admittance of the lumped wall. Note that this procedure measures the global discretization error, larger potentially than the per time-step error.
Using this procedure for typical lightweight residential construction, we have confirmed that the errors in the temperature predictions made by the CSE finite difference algorithms indeed tend toward zero as Δt and Δx are reduced toward zero.
The lumped layer thickness, Δx, should be is chosen thin enough that the single temperature of the lumped layer is a good measure of the average temperature over a width Δx of the sinusoidal temperature distribution in the material. That is, the temperature of the sinusoidal wave should not vary much over the layer width. This criterion is similar to that used by Chirlian (1973) to determine the appropriate lump sizes in electrical circuits.
The wave length of the temperature distribution in a particular material is given by
Equation 31
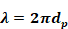
where dp , the penetration depth, an intrinsic characteristic of the material, is given by
Equation 32
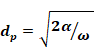
where the angular frequency , ω=2π/period α is the thermal diffusivity of the layer material, and ω is the highest angular frequency of the environmental boundary conditions for which good frequency response is desired. As a general guideline it is suggested that the lumped layer thicknesses, Δx, be chosen to be thinner than the penetration depth for the layer. That is, select
Equation 33
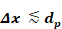
Substituting Equation 32 into Equation 33 shows that the rule of Equation 33 limits the lump size Δx to about 16% of the wavelength:
Equation 34
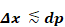
The Equation 33 rule is more important for the modeling of
layers on the inner side of the wall, where the layers are subjected to the
higher frequency harmonics of inside driving conditions. Deeper into the wall
the high frequency harmonics begin to be damped (by about a factor of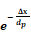
so accurate modeling is of less significance.
The time step used in the code is input by the user. For high accuracy Equation 7 and Equation 14 should be applied using a time step that is a small fraction of the smallest time constant of any layer.
Equation 35
Δt≪τ
Thin layers of a material have a smaller time constant τ than thick layers. The time constant of a layer scales as , ∼β^2 where β Is the a layers dimensionless thickness defined as β = Δx/d_p. Thus, if a layers dimensionless thickness is reduced by a factor of two, the time constant is reduced by a factor of four. Therefore the time to run an annual simulation can increase rapidly for small β’S. Small tau layers have cv increased such that tau = dt.
Note that the Euler mass
layer update algorithm of Equation 7 becomes unstable when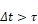
. The
predicted temperatures will oscillate with increasing amplitude each time step.
The code outputs warnings whenever a mass node update is performed for which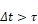
Like the explicit Euler method, the implicit differencing used at the air node is most accurate for small time steps relative to the air's time constant (Equation 12). The implicit difference method is never unstable, and time steps larger than the air time constant give useful, if somewhat inaccurate predictions. The air balance could have been solved using an Euler difference, but since the air time constant is likely the smallest in the zone, it would dictate smaller time steps than is afforded using the implicit method